Area, perimeter, surface, volume of shapes (Geometry)
Area of plane shapes
Triangle, square, rectangle, parallelogram, trapezoid, circle, ellipse, sector.
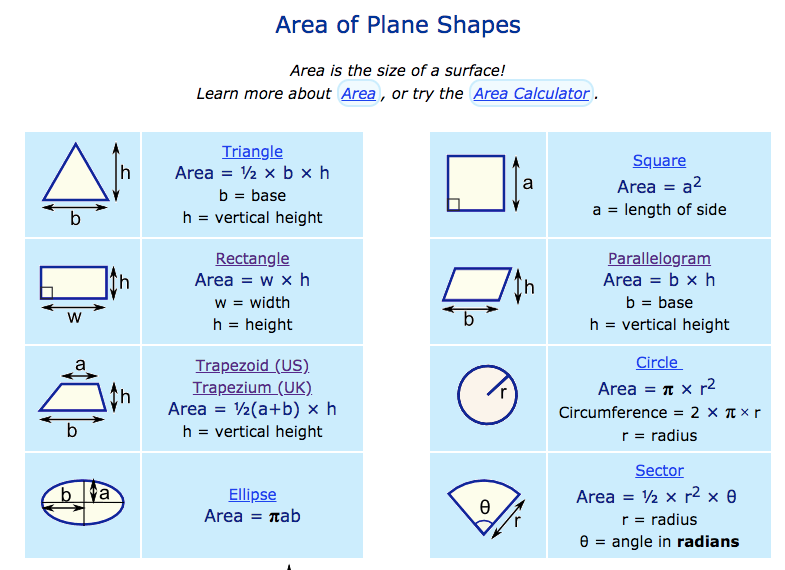
Areas:
- Area of Equilateral Triangles:
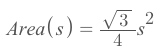
- Isosceles Right Triangle:
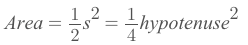
Surface Area
- Surface of Cylinder:
2π · r · (r + h) - Surface of Sphere:
4π · r² - Surface of Cone:
π · r( r + √(h²+r²) )
Volume of Cuboids, Rectangular Prisms and Cubes
Volume = Length · Width · Height
Volume of Cone, sphere, Cylinder
The volume of a Cylinder is: π · r² · h
The volume of a Cone is: 1/3 π · r² · h
The volume of the Sphere is:4/3 π · r³
Refer to math is fun: cone-sphere-cylinder
Volume, surface area of Pyramid
Refer to math is fun: pyramids
- The Volume of a Pyramid:
1/3 · [Base Area] · Height - The Surface Area of a Pyramid:
- When all side faces are the same:
[Base Area] + 1/2 Perimeter · [Slant Length] - When side faces are different:
[Base Area] + [Lateral Area]
Surface Area Formulas and Volume Formulas of 3D Shapes

Surface area formulas and volume formulas appear frequently in geometry, physics, engineering, and everyday problem solving. Whether you’re calculating pressure (force per area), density (mass per volume), or filling a container, knowing these formulas is essential.
Tables for Quick Reference
Here are formulas for quick reference. Full descriptions follow.
Volume Formulas Table
| Shape | Volume Formula |
|---|---|
| Sphere | (4⁄3)πr³ |
| Cube | a³ |
| Rectangular Box | L×W×D |
| Prism | B×h |
| Cylinder | πr²×h |
| Pyramid | (1⁄3)B×h |
| Cone | (1⁄3)πr²×h |
Surface Area Formulas Table
| Shape | Surface Area Formula |
|---|---|
| Sphere | 4πr² |
| Cube | 6a² |
| Box | 2(LW + LD + WD) |
| Prism | 2B + Ph |
| Cylinder | 2πr² + 2πr×h |
| Pyramid | a² + 2a×s (square base) |
| Cone | πr² + πr×s |
🟠 Sphere Surface Area Formula and Sphere Volume Formula
A sphere is a perfectly round 3D shape where every point on the surface is equidistant from the center. The distance is the radius, r.
- Surface area = 4πr2
- Volume = (4⁄3)πr3
🧊 General Prism
A prism is a geometric shape consisting of a stack of identical base shapes stacked on top of each other to a depth d. This prism is a prism formed by a stack of triangles.
- Surface Area of a Prism = 2 × (Area of the base shape) + (Perimeter of base shape) × (d)
- Volume of a Prism = (Area of base shape) × d
Need to find the area and perimeter of the base shape? Use the Area Formulas and Perimeter Formulas.
🧱 Rectangular Prism (Box)
A box or rectangular prism is a stack of rectangles L long and W wide piled on top of each other to a depth of D.
Surface Area of a Box = Sum of the areas of each face of the box
- Surface Area of a Box = 2(L × W + L × D + W × D)
- Volume of a Box = L × W × D
🔲 Cube
A cube is a special case box where all the sides are the same length (a).
- Surface Area of a Cube = 6a2
- Volume of a Cube = a3
🥫 Cylinder
A cylinder is a prism where the base shape is a circle. It has bases of radius r and height h.
- Surface Area of a Cylinder = 2πr2 + 2πrh
- Volume of a Cylinder = πr2h
🔺 Square Pyramid

A pyramid is a solid shape consisting of a polygon base and triangular faces meeting at a common point above the base. A square pyramid is a pyramid where the base polygon is a square.
In the picture above, side a is the same length as side b. All of the face triangles are isosceles triangles meeting at a point h above the base.


For pyramids with identical face triangles (a = b = c)


The math is easier using the slant height (c) rather than the height (h):
- Surface Area = a² + 2as
- Volume = (1⁄3)a²h
🧁 Cone

A cone is a pyramid with a circular base with radius r and height h. Rind the side length or slant height (s) using the Pythagorean Theorem.
s2 = r2 + h2
or
s = √( r2 + h2 )
- Surface Area of a Cone = πr2 + πrs
- Volume of a Cone = 1⁄3( πr2h )
CR :: https://medium.com/all-math-before-college/area-perimeter-surface-volume-of-shapes-geometry-cb8e702c2dc8 , https://sciencenotes.org/surface-area-formulas-volume-formulas/








